Connected components

A connected component of an undirected is a set of nodes, wherein it is possible to get from any node \(i\) in that set to any other node \(j\) by traversing the edges of that network. A network is fully connected if it has one connected component.

import numpy as np
from graspologic.simulations import sbm
from graspologic.plot import heatmap

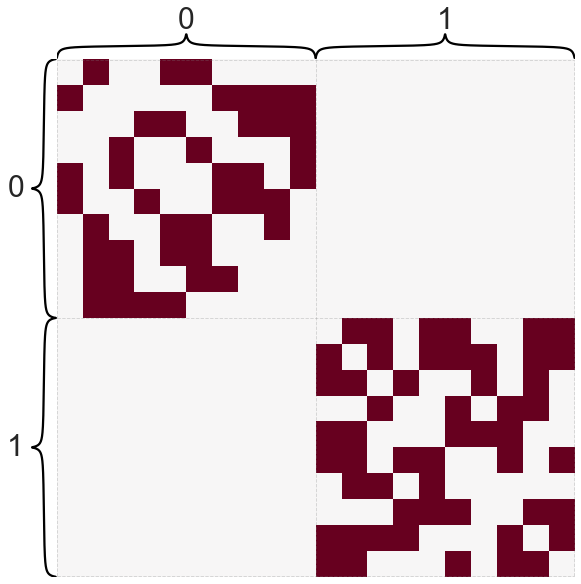
A, labels = sbm([10, 10], [[0.5, 0], [0, 0.5]], return_labels=True)

heatmap(A, inner_hier_labels=labels, cbar=False)

<AxesSubplot:>

graspologic has tools for dealing with connected components. First, it is often useful to know whether a network is fully connected.

Note

For most applications, if your graph has multiple connected components, it makes more sense to treat each component as its own network and to analyze them separately.

from graspologic.utils import is_fully_connected

is_fully_connected(A)

False

import networkx as nx

g = nx.from_numpy_array(A)
is_fully_connected(g)

False

for component in nx.connected_components(g):
    print(len(component))

10
10

For a directed network, there are two notions of connectedness.

• A weakly connected component is a set of nodes such that it is possible to get from any node \(i\) in the set to any node \(j\) in the set while ignoring edge directions.

• A strongly connected component is a set of nodes such that it is possible to get from any node \(i\) in the set to any node \(j\) in the set.

Strong connectedness implies weak connectedness.

Strictly speaking, you have to specify which version of connectedness you mean when talking about directed networks. However, I think it’s more common to assume people mean weakly connected.

This is the version of connectedness for a directed network that graspologic means.

A, labels = sbm([10, 10], [[0.5, 0], [0, 0.5]], return_labels=True, directed=True)

is_fully_connected(A)

False

g = nx.from_numpy_array(A, create_using=nx.DiGraph)

nx.is_weakly_connected(g)

False

For data cleaning purposes, it is often helpful to be able to select the largest connected component. Just like it sounds, this is just the largest group of nodes in the network which satisfy one of the connectedness properties above.

from graspologic.utils import largest_connected_component

A = sbm([20, 10], [[0.5, 0], [0, 0.5]])

A_lcc = largest_connected_component(A)
A_lcc.shape

(20, 20)