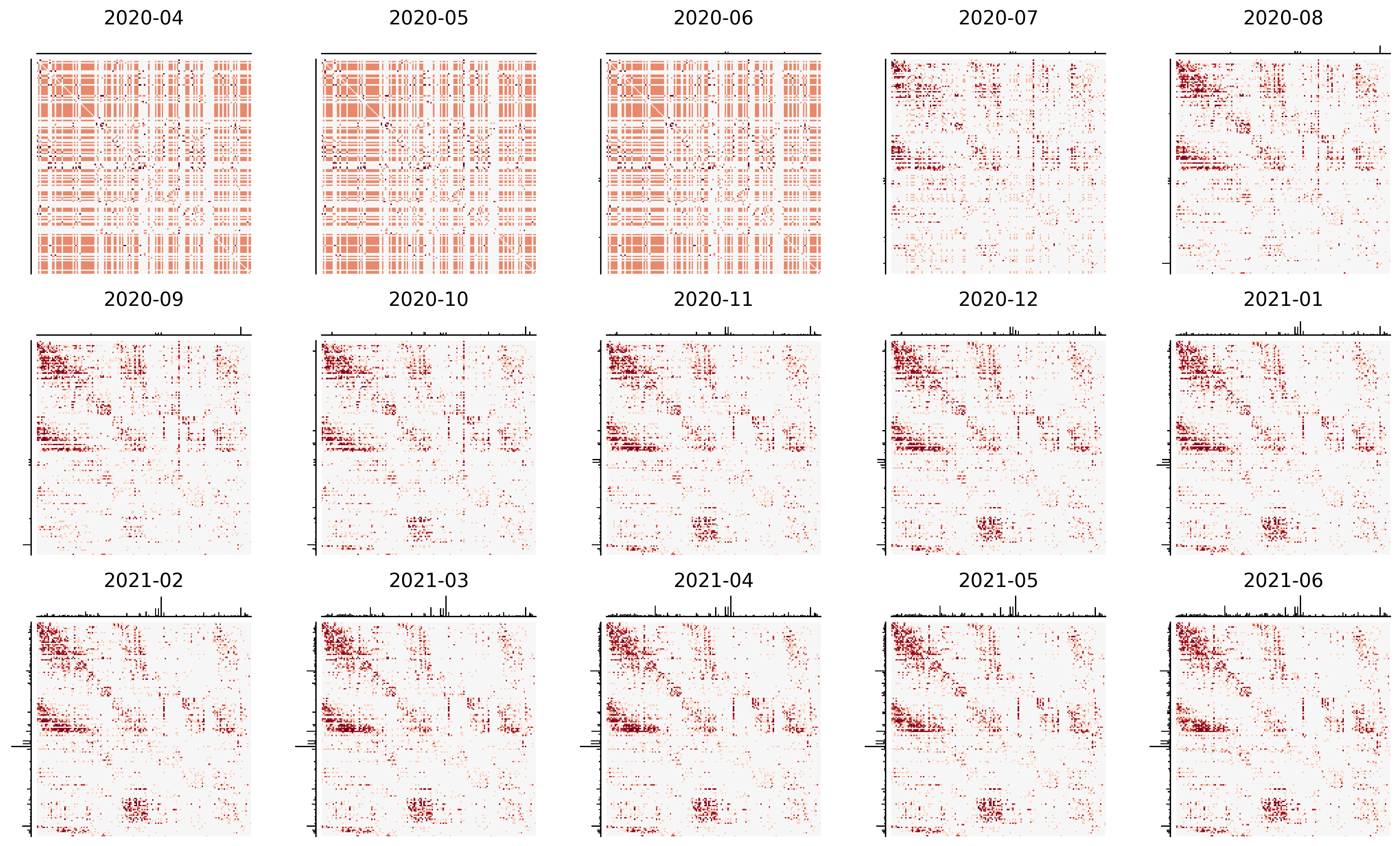
Network-wise statistics
Statistics computed on the entire network - here, an induced subgraph of inhibitory neurons on 163 nodes.
Historical ordering
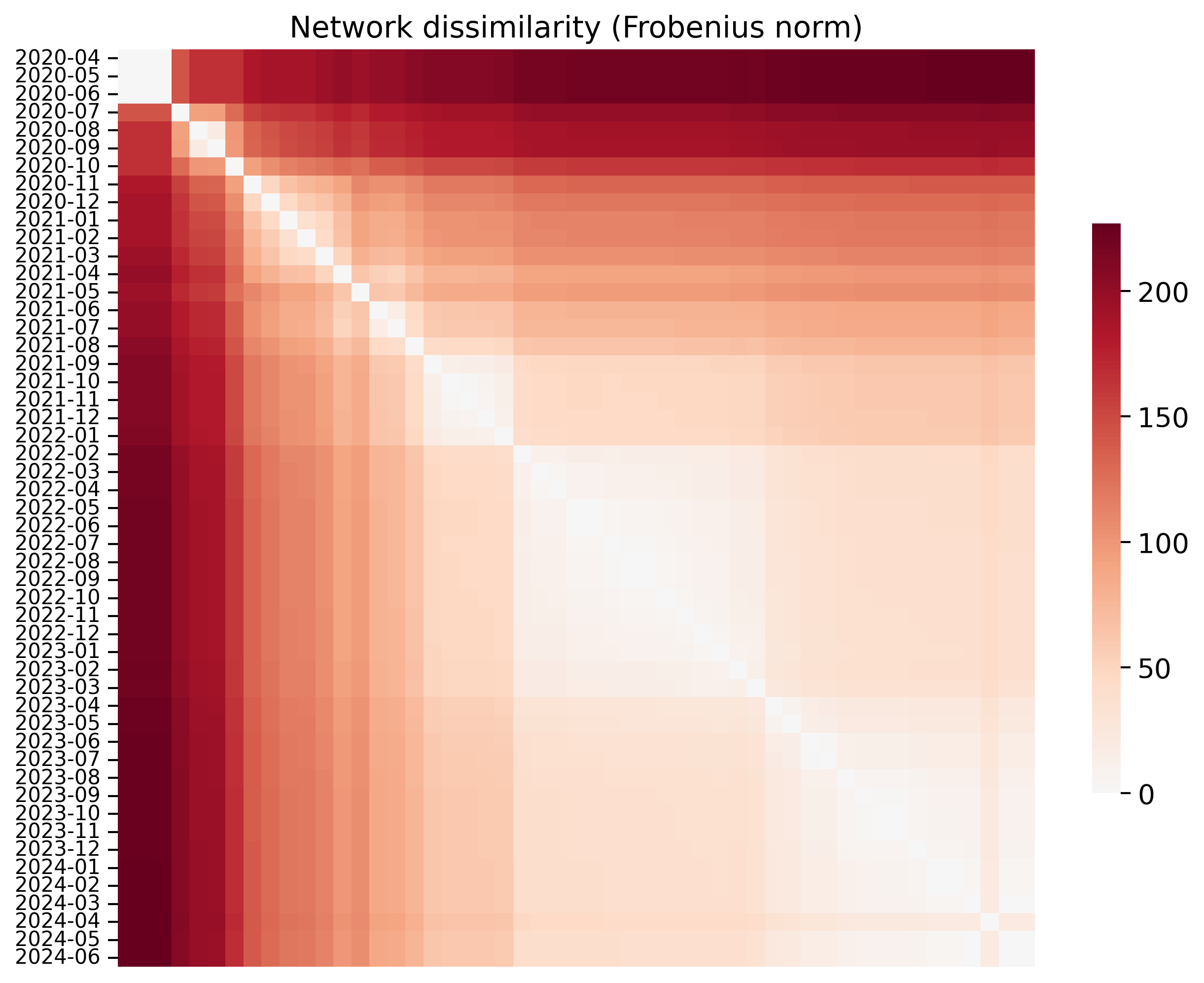
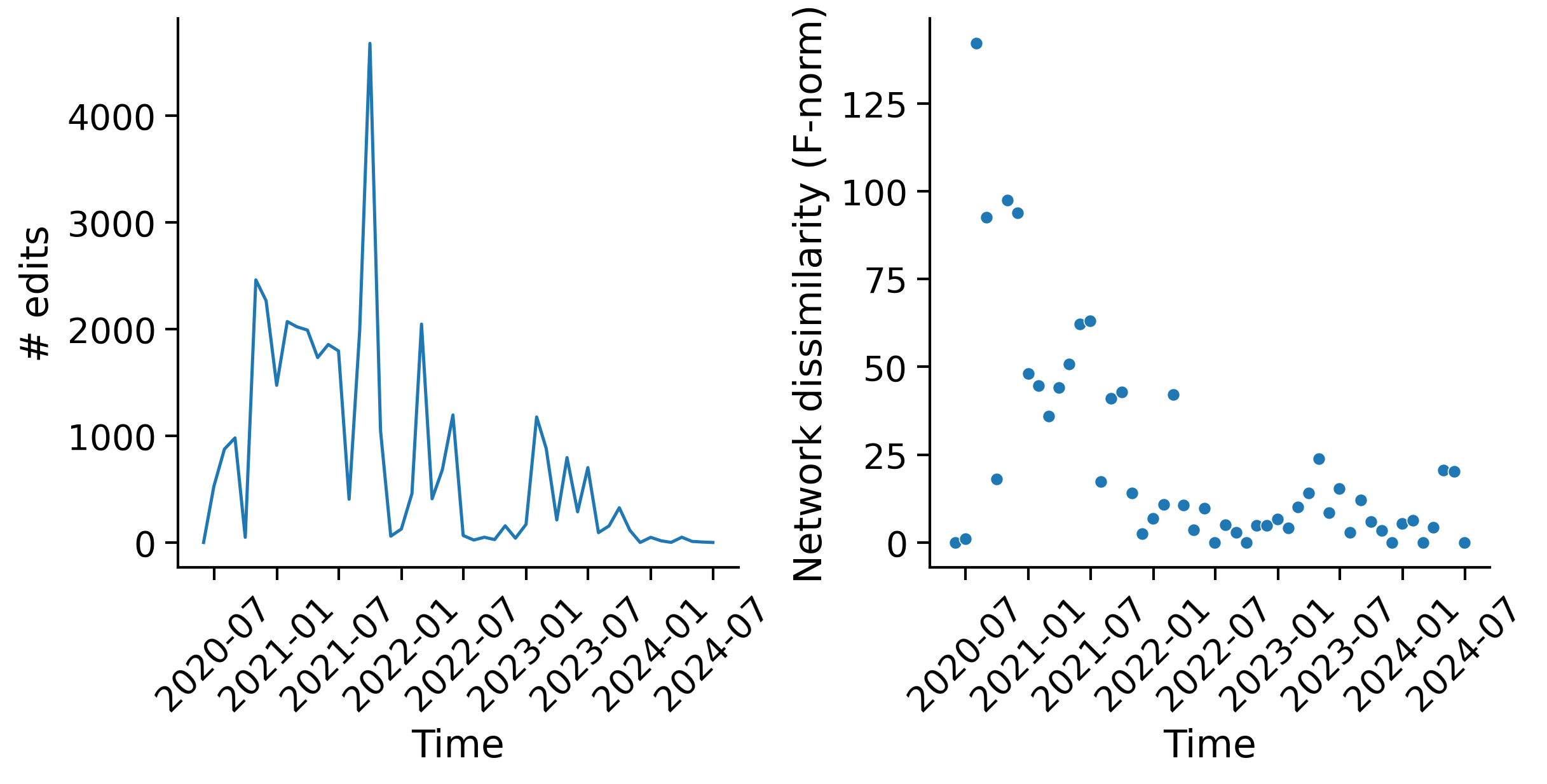
Network dissimilarity: for the simplest notion of the difference in network structure over time, I define a network dissimilarity as:
\[\|A^{(t_1)} - A^{(t_2)}\|_F\]
where \(\| \cdot \|_F\) is the Frobenius norm, i.e. treating the matrices as vectors and taking the Euclidean norm. Intuitively, this metric just measures the magnitude of edge weight changes.